Exploring a Different Way of Learning

Hello AMEP Blog readers!

I’m Pete Cosgrove, a year 6 teacher at St Joseph’s Catholic Primary School in Pinjarra.

When the children see the whiteboards set up before the maths lesson and they understand it’s going to be a problem-solving session, there is a lovely excited buzz as they enter the classroom. This is a Year 6 class with minimal behavioural issues – twenty years in the classroom and I struggle to recall a nicer bunch.

Classroom Example

Problem: In a quadrilateral, Angle A is half the size of Angle B, which is half the size of Angle C, which is half the size of angle D. Calculate the size of the angles and sketch the quadrilateral.

We have a brief Launch Phase around the properties of a quadrilateral to ensure that everyone will be able to tackle the question – they can. We then quickly revisit some guidelines for the group work. In particular, we discuss the necessity that the members of each group should ask a classmate to justify their ideas and any possible solutions.

Often at the start of a maths lesson, the pattern will follow ‘I do, we do, you do’. We avoid that here.

I have anticipated that the children will use the ‘Guess & Check’ strategy with which they are familiar and hopefully work systematically towards a solution. It is an outside bet that someone might use some form of algebraic method (b=2a etc) but I do not expect it.

The problem-solving begins and I am pleased to see that the (genuinely random) groups are all busily engaged in the task.

After ten minutes or so, two groups appear to have stalled and have not settled into a systematic method so I provide them with the ‘enabling prompt’ which is for them to try an angle size for Angle A, the smallest angle, and work from there to see what the sum of the four angles would be (and whether that is higher or lower than 360).

After another ten minutes, a triumphant shriek goes up from the first group to solve it. They have used ‘Guess & Check’ and worked systematically thereafter to the solution.

I give them the extension task: What if Angle A was 1/3 of Angle B, which was 1/3 of Angle C which was 1/3 of Angle D? (They do get to solve this in the time left.)

One other group solves the original problem but due to a calculation error, do not realise that they have been successful.

I decide to not explore the possible algebraic method at this point.

In the Discussion Phase that followed the group-work, a few interesting things emerge. The groups who have not managed to solve the problem have used ‘Guess & Check’ but after trying some values for Angle A, do not stick with it, and instead try a range of other ideas suggested by a group member.

Some of these ideas originate from pupils regarded as the better mathematicians by other group members, (despite not necessarily being the better problem solvers). Rather they are conscientious and will reliably apply a taught strategy to similar questions. One pupil, who’s confident in her mathematical ability, is a member of a group unable to solve the problem and appears put out to have been beaten to the chase.

The lesson ended before the children had the time to draw the quadrilateral. The following day, the class had the opportunity. There were some successes, but the majority were unsuccessful.

Generally, it was the fact that Angle D was a reflex angle that was the sticking point. They did know how to draw a reflex angle but the fact that the angle created a chevron-like quadrilateral meant they were inserting it as the external rather than internal angle to create a more ‘normal’ looking quadrilateral.

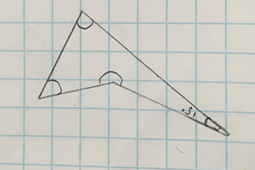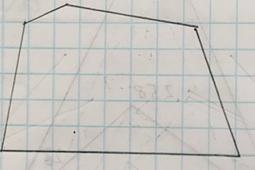The other sticking point was because they knew the size of all four angles, they were measuring and drawing all four, without realising the fourth angle would take care of itself if the other three were drawn correctly. This meant a puzzled few ended up unintentionally drawing pentagons.

From a teacher’s perspective, these Champions of Maths group problem-solving sessions have proved beneficial for both teaching and learning.

Random Groups

In their daily maths lessons, the children are generally grouped by ability. We do a fair bit of partner talk in the lesson. There are some maths lessons where they work in mixed ability pairs but generally, I’m wary. I’m wary that the lower ability child can lean too heavily on their partner rather than working independently. Also, I feel that a higher ability child should be extended rather than be responsible for explaining a task to a classmate. So, these fortnightly sessions, where the children work in groups irrespective of ability are a change to that norm. And they do work – perhaps due to the problem-solving nature of the task cutting across the usual ability bands.

Perhaps my usual scepticism around group work is not that I don’t see the benefits and I feel these benefits can sometimes be overplayed. Absolutely, I feel children need to develop skills for working productively in a team. However, equally important for me is the need to develop a child’s ability to work independently and take personal responsibility for their part of the task in hand.

These Champions of Maths sessions have moved my thinking somewhat. They give the children a chance to explore a different way of learning (and me a different way of teaching) and that has benefited everyone.

Selecting the Task

I feel this is key to a productive session. All the children have to feel that they can solve the problem to remain engaged. Yet, it needs simultaneously to be a challenging enough task. Personally, I’ve found that problems that combine elements of geometry and numbers seem to work well.

Discussion

The idea of the Explore section of the lesson being a build-up or prelude to the main part, with the Discussion at the end, is novel for me. I think I have previously been guilty of not putting enough thought into the construction of this part of the lesson. I now feel that I’m thinking more about which child/group to feedback to across all subjects. The quality of the discussion has improved.

Teacher Workshops

Maybe I’ve just got lucky with the teachers involved in this program, but the quality of the teacher workshops has been refreshing. Shyam definitely knows his stuff. It has also been blessedly ego free with teachers as ready to share where their lessons didn’t quite go to plan as their successes. Working as a teacher in a one form entry school, it has been really beneficial listening to colleagues from other schools who are generous and willing to share their ideas and experiences. A two-hour workshop after school on a winter’s evening is usually the stuff of nightmares. But, genuinely, the time flies!

Find out more about the Alcoa Maths Enrichment Program or read the next article.

Would you like to continue a discussion on this topic with other educators? Join our Facebook group!

If you are interested in joining the Alcoa Maths Enrichment Program please fill out the enquiry form below and a Scitech representative will be in touch with you.