Connected Learning

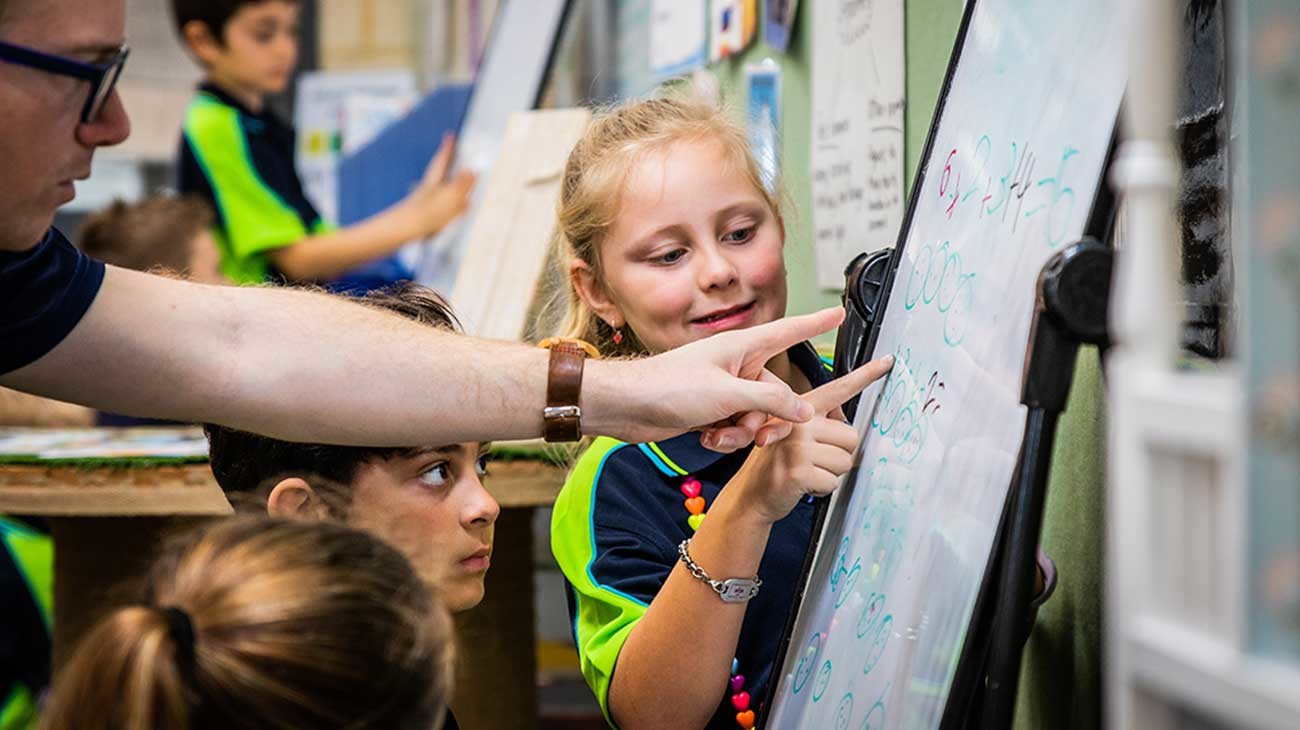
Hello everyone, my name is Karl Schoeppner and I am a Year 5/6 Teacher at Oakwood Primary School.

I have always considered myself quite good at mathematics, yet I wonder why it is I have found teaching maths concepts so difficult at times. I’ve found teaching problem solving skills a challenge as often the best approach changes depending on the problem at hand. The Alcoa Champions on Maths program has really opened a new world of teaching for me, that has helped progress my students with challenging learning.

This year I have a large class of Year Five and Year Six students who have been learning mathematical concepts and problem-solving skills thanks to this program.

In the past I have felt problem-solving could be tackled in two ways. Firstly, students could work through word problems independently, however, they often found the idea of sitting and reading a bunch of problems usually with repetitive operations, dull. The second option was providing students with creative problems that relied on deep mathematical understandings that they often struggled to solve independently. No matter who I spoke to, I couldn’t find a more effective method of teaching students to solve problems.

Enter Shyam Drury and Champions of Maths.

Let me describe one particular lesson which focused on reinforcing the concept of area. I had two pretty clear groups of students – those who had a fairly strong grasp of area and the expectations for Year Five and Six students and another group that still had trouble picturing the concept, let alone applying any formula. As a result, I chose a question where students would have to practice solving area of many rectangles as well as an opportunity for students to practice finding efficiency in solving problems.

Students were asked to look at a rectangular prism of dimensions 3cm by 4cm by 5cm. “I want to paint the whole prism. How many square centimetres of paint will I require? My paint tin covers 140cm², do I have enough paint?”

A massive part of the program I love is the engagement from the students. The class are focussed and determined to solve the problem. A large portion of the groups managed to solve the problem though even those who didn’t find the answer managed to develop their mathematical thinking. But, it is the plenary where I found the greatest progress is made. I strategically chose a range of student work to discuss as a class. Group members were provided opportunities to share what they had achieved and where they struggled. Two groups I strategically selected had come close to getting the answer and the other two groups got the answer in different ways. The whole class were very supportive and, with all students knowing how challenging the task was, showed respect to all presenting.

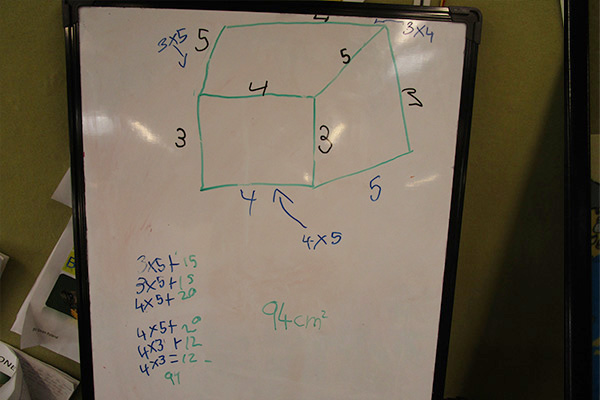
Student solutions:

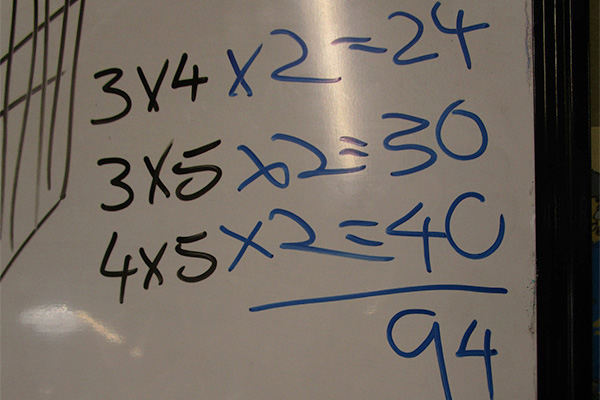The first group, who made the least progress on solving the problem, shared what they had. The group talked about how they had looked at the width and length to find the area of two sides. As a class we celebrated this with the group. It was a starting point for them to see what they had done well. I asked the question: “Have you looked at all sides of the shape?” To which the group was unable to answer.

We moved onto the second group, who had made greater progress yet still didn’t have an answer. I asked the group to explain what they had done.

One student stated, “We drew dots instead of squares. This made it look like an array for us.”

By connecting the idea to arrays (a topic they were familiar with) students were able to deepen their understanding of area. I did a small bounce back to the first group and commended them on seeing this for the two sides they had solved.

The final two groups then shared. I started by asking, “Instead of looking for the right answer, I’m after what is the fastest or most efficient way to solve this problem.”

The first group explained their strategy which involved solving a side and then doubling it (to take into account the opposing side) and adding all sides together. I was able to stop at this point and ask the class, “I can see many similarities between the third board and the first. Can anyone see what the first group missed?” Although I asked the whole class, I was excited to see a member from the first group offer an answer and explain they had missed one edge and the opposing sides.

The fourth and final group to share showed a strategy in which they solved all six sides individually. Our final discussion looked at how the group that used doubling was more efficient as the process took less steps and had less chance for error.

By asking strategic questions, I was able to draw students attention to and help all students see the evolution of their thinking to the next step. Students could connect and explain how a concrete idea like counting the squares on the prism could be simplified to an array. Or, how opposing sides were the same and were not required to be calculated twice.

One of my greatest “Wow” moments from this program came in a simple question, “Having seen what these groups have done; can you see a more efficient method?”

The class sat in thought for a moment, then one student who I did not expect to answer, identified the possibility of factorising the problem, “Could you add up three of the sides and then double it?”

For me, this is where the power of the program comes into play. I love the team work students have developed with each other, I love the way stronger students have begun taking the time to ensure the whole group understands mathematical strategies, I love the way differentiation is naturally built into the program. Through the way students can build connections in their work and the work of others is powerful. The ability for students to connect the concrete to the abstract and use it in their future work has helped my class grow considerably. When I look back at the way I use to teach problem solving skills, I can’t believe the growth I’ve made in such a short time.

Find out more about the Alcoa Maths Enrichment Program or read the next article.

Would you like to continue a discussion on this topic with other educators? Join our Facebook group!

If you are interested in joining the Alcoa Maths Enrichment Program please fill out the enquiry form below and a Scitech representative will be in touch with you.