Is Reasoning at the Heart of Maths Proficiency?

This is Leanne Northey, Year 6 teacher from Ocean Road Primary School, with my second Champions of Maths blog post for the year. You can read my first one here.

I’d like to discuss my student’s experience with learning mathematical reasoning.  One of our workshops explained how reasoning is linked to problem-solving and is needed during the problem-solving process. Mathematical reasoning underpins all mathematics and, in my opinion, is the most important part of the maths curriculum, but is the proficiency that is often neglected! The Australian Curriculum states that students are reasoning “when they explain their thinking, when they deduce and justify strategies used and conclusions reached, when they adapt the known to the unknown, when they transfer learning from one context to another, when they prove that something is true or false, and when they compare and contrast related ideas and explain their choices” (Australian Curriculum, Assessment and Reporting Authority, 2017).

“Which one doesn’t belong” has long been a favourite warm up of mine and my class were familiar with identifying and describing common properties and attempting to communicate a rule with evidence. For example, when presented with this image, the responses may be:

“the 9 doesn’t belong as it is the only single digit number”
“the 16 doesn’t belong because it is the only even number”
“43 doesn’t belong as it the only number that is not a square number”

I wanted my students to move from just describing and explaining to be able to justify with evidence, refute claims and prove the validity of statements.

ReSolve has developed a range of tasks aimed at assessing reasoning and identified three main reasoning actions – Analysing, Generalising and Justifying. A rubric, along with work samples for each of the tasks was an extremely useful resource.

One of the first tasks that we did was “What else belongs”.  The task was:

Could these numbers 36, 12, 18 belong together? Why?

What other numbers do you think could belong with these numbers?  How do you know that all these numbers fit with your reason? Use words, numbers or drawings to explain

Students were able to analyse and notice a pattern and generalised using mathematical terms. They identified that the numbers belong together because they are even, are composite numbers or are multiples of 3 or 6.  When asked what other numbers belong with this group, students were able to state other numbers that fit with the same reasons. For example, 2 and 10 also fit because they are even. This showed that students were generalising as they were explaining how the rule works with examples.

One of our activities after one of the workshops was to conduct the ReSolve ‘Number Towers’ task, assess the reasoning and bring it back to the next workshop for moderation.  The task was as follows:

Place the numbers 1 – 5 in the bottom row of the number tower. Add each pair of numbers together to make the numbers in the next row up.  Repeat this until you have one number at the top.  Your task is to make the largest total at the top of the tower.  Try different arrangements and look for a reason to explain your findings.

My learning goal for this task was for my students to make a conjecture about the position of the numbers in the bottom of the tower and justify their placement with examples.  Through moderation of the assessment task, I observed that some students were developing their justifying skills when they attempted to verify by testing cases (e.g. “the smallest numbers had to be away from each other to get the largest number”) and starting to use a correct logical argument (“put the smaller numbers on the outside of the tower as they don’t get used  as much when adding”)

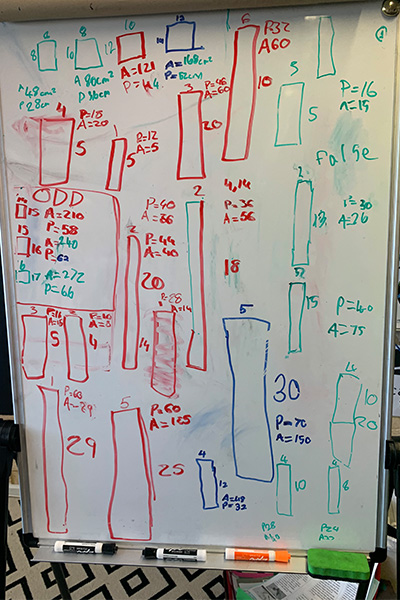
Another reasoning task focused on the idea that you only need one counter example to disprove a conjecture. The Area and Perimeter task was:

Nathan said: “When you increase the perimeter of a rectangle, the area always increases.”
Is this statement true for all cases?
Explain, with examples, why Nathan’s statement is correct, or incorrect.

Students moved on from testing if the conjecture was true, to proving that it wasn’t.

One of our last tasks, the Painted Cube, was not only hands-on and engaging, but allowed students to visually see what was happening to help them test conjectures.  Several examples of justifying were evident with watertight logical arguments provided (“the number of cubes painted on 3 faces will always be 8, no matter what the size of the cube, because every cube has 8 corners).

During the numerous reasoning tasks that my class participated in this year, students started to use more refined logic and rational thinking.  I was able to see a progression in reasoning skills from describing and explaining through to convincing, justifying and proving.

Problem-solving and reasoning tasks encourages students to believe in their ability to be users of maths and help them make sense of maths they encounter.  Reasoning tasks don’t always have to be an explicit lesson but can be embedded in all maths lessons through careful and considered prompts and questioning. I am looking forward to continuing with my new skills in the future.

Find out more about the Alcoa Maths Enrichment Program.

Would you like to continue a discussion on this topic with other educators? Join our Facebook group!

If you are interested in joining the Alcoa Maths Enrichment Program please fill out the enquiry form below and a Scitech representative will be in touch with you.